Exploring Aristotle's Wheel Paradox: A Mathematical Journey
Written on
Chapter 1: Understanding the Paradox
Have you ever pondered over the complexities of Aristotle’s Wheel Paradox? This captivating mathematical dilemma involves four concentric circles within a rigid wheel, appearing to complete a full revolution as they traverse four equal segments. One might hastily conclude that since the horizontal lines are of equal length, the circumferences of the circles must also be identical. However, this assumption is fundamentally flawed, as anyone can discern with a cursory glance.
The crux of the matter lies in a crucial presumption: the rigid wheel genuinely performs a complete revolution. Before you proceed, I encourage you to pause, grab some paper, and attempt to solve the paradox. Ready? Let’s delve into the solution!
A Brief Overview of Aristotle’s Wheel
To fully grasp this fascinating paradox, we must first explore its historical roots. Aristotle’s Wheel is part of the Aristotelian corpus, specifically the collection known as "Mechanica." This work addresses various mathematical and philosophical problems related to mechanics and is traditionally attributed to Aristotle himself.
The illustration seen above is labeled as ‘Problem 24’ and describes the wheel's mechanics. In essence, it discusses two circles—one larger and one smaller—both sharing a common center. As the smaller circle rolls, it supposedly covers the same distance as the larger one. Although this concept may seem convoluted at first, the primary idea remains clear.
To enhance your understanding, let’s take a look at some animations related to this paradox.

Here are two animations illustrating Aristotle’s Wheel Paradox using a wooden puzzle.
The first animation showcases the inner circle sliding atop an outer circle with a larger radius. You’ll observe that as it moves from left to right, a ruler measures the distance traveled, which ranges approximately from 2cm to 6cm.
The second animation illustrates the inner circle moving independently. Interestingly, it traces the same distance (from 2cm to 6cm) as noted in the first animation, where the inner circle rolls over the outer one.
Do you start to grasp the concept? Let’s continue to uncover the fallacy behind this wheel!
Examining the Fallacy with Galileo
The image below depicts a wheel completing one full revolution while transitioning from point P1 to P2. There’s no doubt that the wheel indeed makes a complete revolution. So, how do we resolve this paradox?
Italian polymath Galileo provided an insightful analysis of this conundrum.
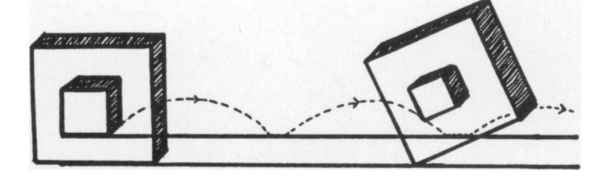
Consider instead two square wheels. As the larger wheel pivots, the smaller one lifts off the ground, resulting in additional horizontal displacement. This cumulative effect of numerous lifts leads to the inner wheel's enhanced movement along the track.

For polygonal wheels with more sides, the smaller wheel experiences multiple smaller lifts as it rotates, similarly contributing to its increased displacement. As we approach the limit of a circular wheel, this results in the inner wheel sliding forward as it turns.

How intriguing, isn’t it? What are your thoughts? I’d love to hear your insights in the comments below!
Thank you for taking this mathematical journey with me. If you enjoyed this exploration, please consider sharing it with your friends or exploring more mathematical puzzles on Medium.

Remember, your engagement is appreciated. If you found this article enlightening, feel free to clap for it!
If you’d like to support my work, consider buying me a coffee. Your generosity fuels my passion for sharing knowledge. Thank you!