# The Heisenberg Uncertainty Principle: A Shift in Understanding
Written on
Chapter 1: Introduction to Quantum Peculiarities
Quantum physics is undeniably perplexing, often defying our conventional understanding of the universe. As scientists delved deeper into this field, they encountered ideas that were increasingly difficult to accept. A pivotal moment came with the introduction of the Heisenberg Uncertainty Principle by the German physicist Werner Heisenberg. This principle established a mathematical boundary on the extent of our knowledge regarding the universe, marking a significant departure from Newtonian physics. Let's examine what this principle conveys and its far-reaching implications.
The Mathematical Framework
Despite its fame and revolutionary impact, the Heisenberg Uncertainty Principle is expressed through a relatively straightforward equation:
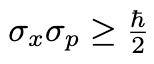
In this equation, the two symbols on the left represent our uncertainties in determining a particle's position and momentum. A larger uncertainty indicates a lack of clarity about these values. In physics, our goal is often to minimize uncertainty. The peculiar symbol “h” on the right stands for the reduced Planck constant, a prevalent figure in quantum mechanics that appears in numerous contexts. Essentially, this equation asserts that the product of these two uncertainties can never fall below a certain threshold. Thus, if we gain precise knowledge of a particle's position, our ability to ascertain its momentum is severely restricted.
This notion contradicts our intuitive understanding! Surely, we can ascertain the location of an object? However, like many concepts in quantum mechanics, grasping this fundamental limitation can be challenging. This principle becomes significant only at the minuscule scale of quantum particles, a realm that is far removed from our everyday experiences.
The Implications of the Principle
The Heisenberg Uncertainty Principle is often regarded as a cornerstone of quantum mechanics, sometimes referred to as the “essential core” of this theoretical framework as it outlines crucial governing rules. At its core, it suggests that particles cannot be viewed as precise points, but rather as waves.

This wave embodies information regarding both the particle's position and momentum. If we achieve perfect knowledge of the position, the wave collapses to a single point, making momentum indeterminate. Conversely, if we precisely determine momentum, then the position becomes elusive. This interplay means that enhancing our understanding of one aspect invariably complicates our grasp of the other.
When designing experiments, physicists must consider this principle. It is an acknowledged limitation that precise knowledge of both position and momentum is unattainable. Richard Feynman encapsulated this idea succinctly in his renowned lectures:
“The uncertainty principle ‘protects’ quantum mechanics. Heisenberg recognized that if it were feasible to measure both momentum and position with greater accuracy, quantum mechanics would collapse. Hence, he proposed that it must be impossible. Many have endeavored to find a method to measure both aspects with improved accuracy—be it a screen, an electron, or even a billiard ball—but none have succeeded. Quantum mechanics continues to exist in its precarious yet accurate state.” — Richard Feynman in Feynman Lecture 37–1
Further Exploration
For those interested in delving deeper into the Heisenberg Uncertainty Principle, I recommend the following resources:
- Stanford Encyclopedia of Philosophy: The Uncertainty Principle. This comprehensive text offers a thorough exploration of the history, mathematics, and interpretations of the principle, albeit in a more rigorous format.
- The Feynman Lectures on Physics — Volume III. Richard Feynman, renowned for his ability to elucidate complex topics, has made his lectures on quantum mechanics available online for free. These lectures are an excellent resource for grasping the concepts surrounding the uncertainty principle and broader quantum mechanics.
I hope this overview has been enlightening! If you appreciate my work, consider becoming a Medium member through this link to support my writing. You can also follow me for more insights into math and science, as I publish weekly on these subjects.