Chapter 1: Introduction to Matrix Square Roots

When we calculate the square root of a number, we seek the value that, when multiplied by itself, returns the original number. This leads to two solutions for square roots, and n solutions for n-th roots, but for now, we will focus on the concept itself.

Extending this idea to matrices, given an n*n matrix A, we aim to determine an n*n matrix B such that B² = A. To simplify our task, let’s first examine cases where the computations are straightforward. The multiplication of diagonal matrices is uncomplicated, as we simply multiply the corresponding entries along the diagonal. Consider this example of a 3*3 matrix:

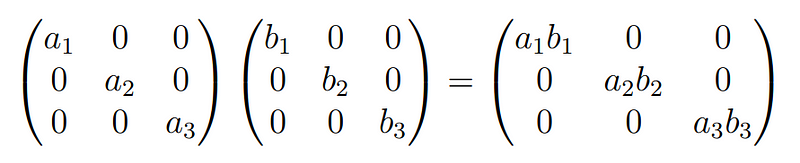
Product of diagonal matrices allows us to find the square root of an n*n diagonal matrix as follows:

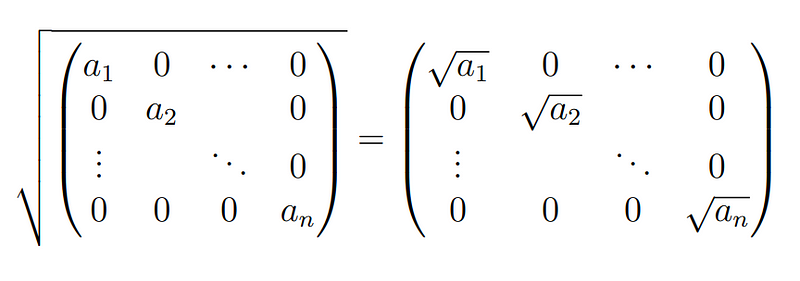
The right side, when squared, will yield the diagonal matrix containing a_1 through a_n along its diagonal. Knowing how to find the square root of a diagonal matrix is beneficial, but we also need a method to transform other matrices into diagonal form. Fortunately, this method exists and is aptly named diagonalization.

To diagonalize matrix A, we must identify its eigenvalues and eigenvectors, defined as numbers λ and vectors v satisfying the equation:

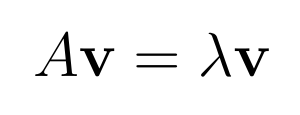
This indicates a vector that the matrix scales by the number λ without altering its direction. Each eigenvector v corresponds to a specific eigenvalue λ.

While I won’t delve into how to compute eigenvalues and eigenvectors here, I might cover it in future discussions. I encourage you to explore this topic in your own time; it becomes quite manageable once understood.

An n*n matrix can be diagonalized if it possesses a complete set of n linearly independent eigenvectors (none of which can be expressed as a linear combination of the others), each associated with a non-zero eigenvalue. After determining the eigenvectors and eigenvalues, diagonalization is performed as follows:

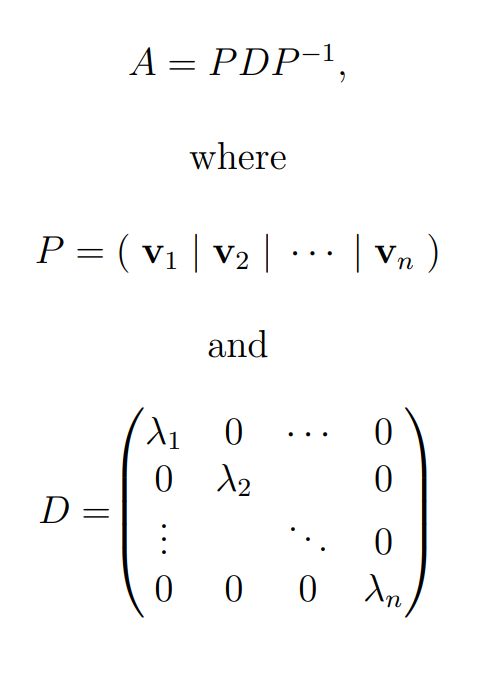
The eigenvectors form the columns of matrix P, while the corresponding eigenvalues populate the diagonal of matrix D.

This diagonal decomposition leads to a useful formula:

For positive integer values of n,

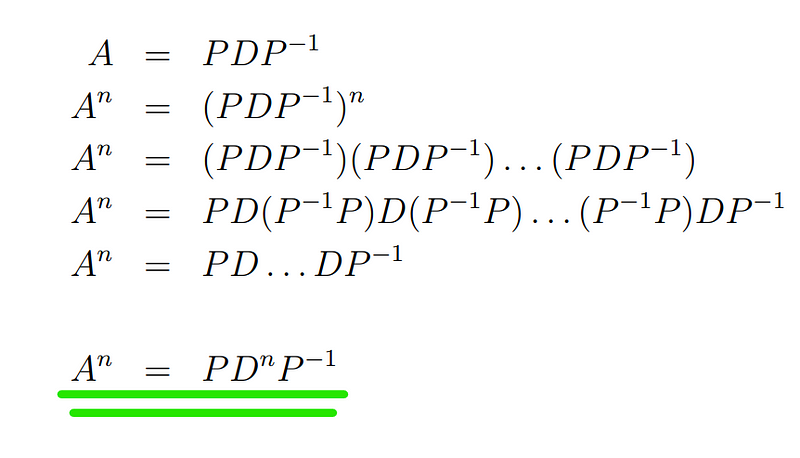
Thus, to compute any positive integer power of A, we only need to calculate powers of the diagonal matrix D, which is significantly simpler. Here’s an illustrative example:

While this method allows us to compute positive integer powers of matrices efficiently, what about fractional powers? We previously noted that we can find a square root of a diagonal matrix; hence, we can also square root the diagonal matrix D from the diagonalization. Let’s explore another example:

Success! We have successfully determined a square root of the matrix. This approach can similarly be used to find cube roots, fourth roots, and beyond. It’s important to mention that we should work within the complex numbers to find square roots of negative eigenvalues.

However, these square roots are not unique. For instance, consider the matrix that represents a 90° counter-clockwise rotation in the 2D plane:

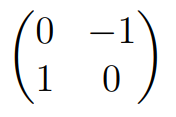
What are the eigenvectors for this matrix? It rotates around the origin in two dimensions, meaning no line remains fixed. This holds true visually. However, since we are operating over the complex numbers, this matrix indeed has a full set of eigenvectors with complex entries, and the corresponding eigenvalues are also complex. The diagonalization method will still yield a square root for this matrix, albeit in a more complex form.

Since the matrix represents a 90° rotation, one might assume another square root could be a 45° rotation. Indeed, this is correct! This square root comprises only real numbers.

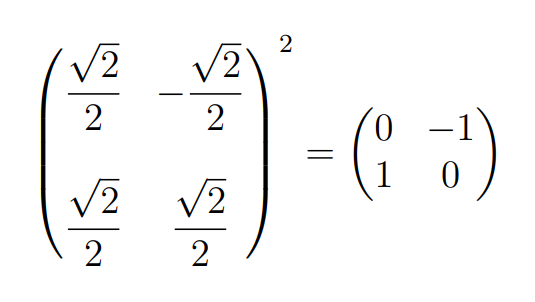
This is a more manageable solution. However, as long as we deal with a diagonalisable matrix, our primary method remains consistently reliable.

Challenge: Identify an infinite set of square roots for the 2*2 identity matrix.

Chapter 2: Video Explanations

In this video, we discuss the concept of finding the square root of a matrix, particularly focusing on the diagonalization process and its implications.

This video offers a deeper dive into the techniques used in linear algebra to extract the square root of a matrix, featuring practical examples and applications.