Chapter 1: Understanding the Geometry Puzzle

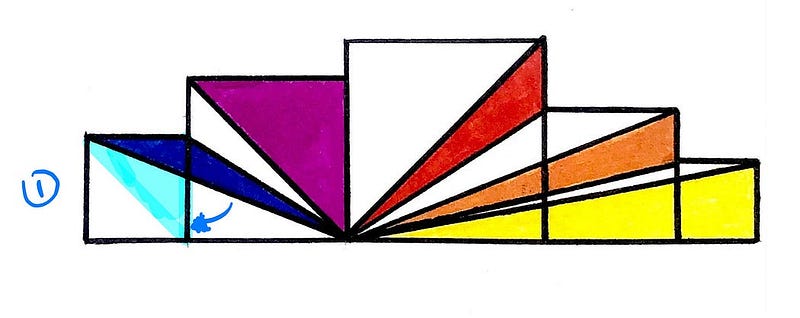
The illustration features five squares with triangular rays converging at a single point. The challenge is to find what fraction of the entire area is shaded. Before I disclose the answer, here's a significant hint for those who wish to attempt solving it themselves.

Does this provide clarity? I suggest pausing to grab some paper and a pen to work through the problem. Once you're ready, continue reading for the solution!

Solution

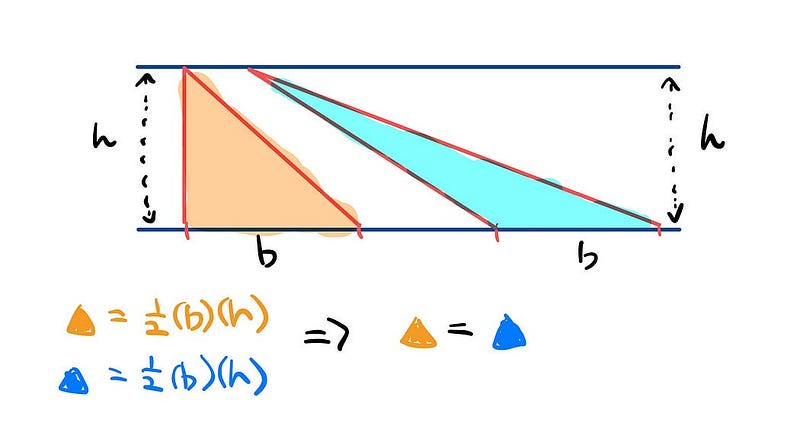
Step 1: We start by moving the tip of the blue triangle along the edge of the squares until it reaches the corner of the first square.

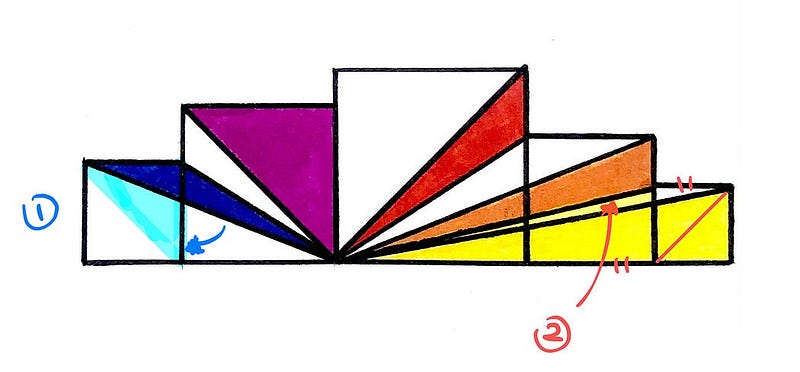
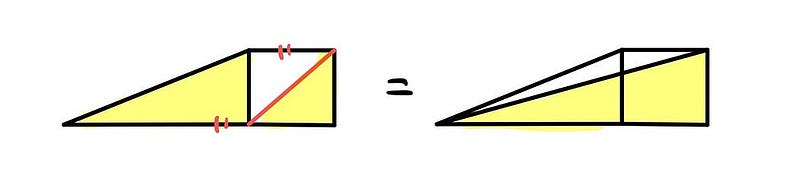
Step 2: This phase involves a bit more complexity. We draw a diagonal on the outermost yellow square and examine the triangle created with the red diagonal.

As we slide the tip of the triangle as in Step 1, it becomes evident that the two yellow regions possess identical areas.

Step 3: This step employs the same logic as in Step 2, but now we focus on the orange section.

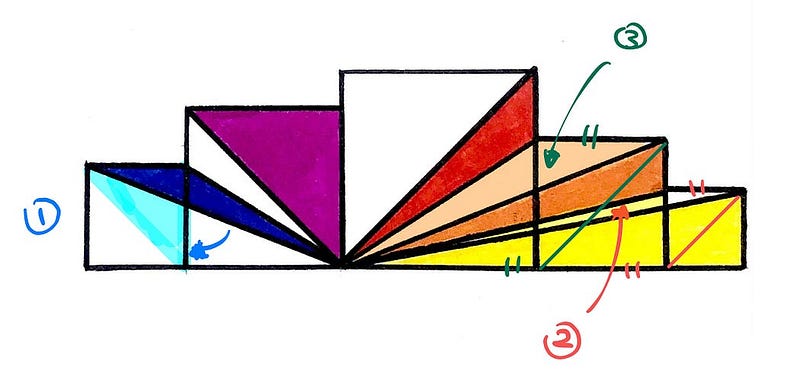
Again, by shifting the tip of the red triangle and considering the original red area in the largest square, the red section occupies half of the square as one triangle.

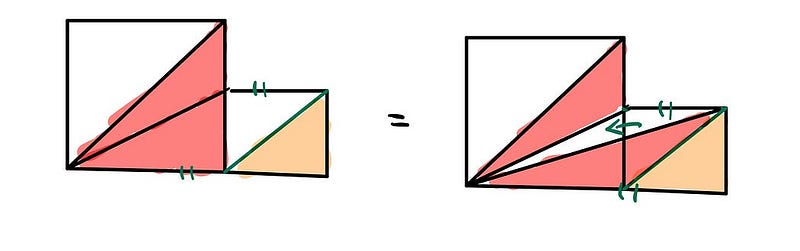
This demonstrates that the shaded area is half of the total figure!

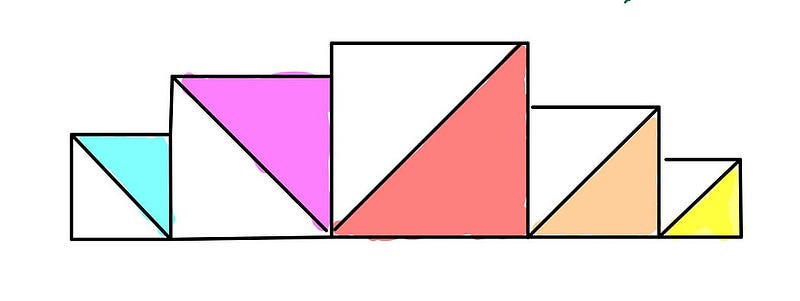
And that’s our elegant solution!

How fascinating is that?

What thoughts crossed your mind while solving this? I would love to hear your insights in the comments below!

Chapter 2: Explore Related Videos

This video demonstrates how to shade fractions of a shape, helping you visualize the concept better.

In this tutorial, you will learn how to shade fractions of various shapes, enhancing your understanding of geometry.

Thank you for your engagement! If you found this article valuable, please clap for it and consider sharing it with friends who enjoy math puzzles.

If you appreciate my efforts, consider supporting my writing by buying me a coffee. Your generosity greatly assists my academic journey and writing endeavors. Happy Solving, Bella!