Chapter 1: Introduction to the Problem

In this segment, we delve into a fascinating number theory challenge from the International Mathematical Olympiad of 1979. This particular problem revolves around the concept of divisibility. Are you ready to tackle this problem on your own? Challenge yourself before peeking at the solution; the satisfaction of solving it independently is truly rewarding!

Rather than hastily summing all the fractions, which might initially seem appealing, we quickly realize that this approach leads us to a dead end. However, an important observation emerges: all the negative terms possess even denominators. This insight directs our next steps. We can reformulate our sum in the following manner:

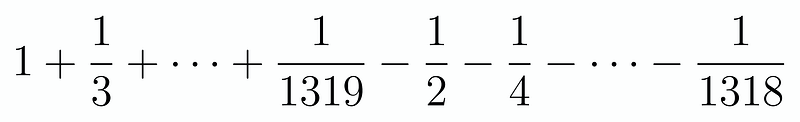
Or, expressed alternatively:

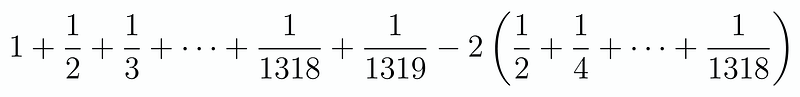
To clarify, we duplicate all the even denominators to create a complete sum on the left side, subsequently subtracting this from the right side. Notably, all the denominators on the right side are also even, leading us to the conclusion that:

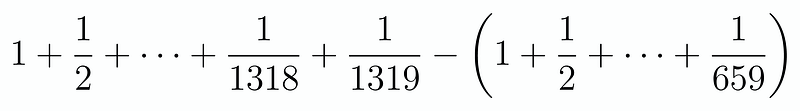
With this transformation, we are left with a significantly simplified sum! We can now eliminate the initial 659 terms, ultimately reducing it to:

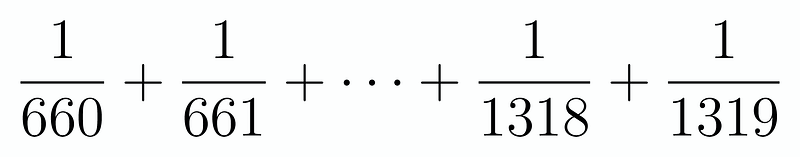
Interestingly, we aim to demonstrate that the numerator is divisible by exactly 1979. Observing the sum of the first and last denominators reveals they equal 1979. Continuing this pattern, the second denominator and the second-to-last also total 1979. This relationship holds true for each pair due to the even number of terms, allowing us to calculate the sum as follows:

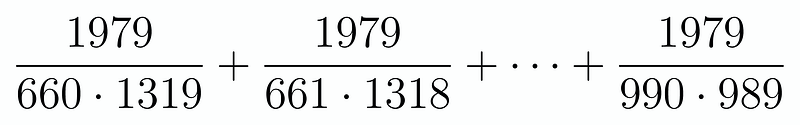
Ultimately, since 1979 is present in every numerator and is a prime number, summing these fractions guarantees a factor of 1979 in the numerator. Consequently, we conclude that ( a ) is indeed divisible by 1979, and our solution is complete.

Enjoyed working through the problem? If you found it helpful, consider showing your support!

If you have an alternative solution, feel free to share your thoughts in the comments below.

Chapter 2: Video Resources

To deepen your understanding of this problem, here are two insightful videos:

The first video, "Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1," provides a concise explanation of the solution process.

The second video, "YOU can do this IMO PROBLEM | IMO 1979 Q1," encourages viewers that with determination, they can also tackle this problem successfully.