Chapter 1: The Integral Dilemma

Recently, I assigned a problem to my students that involved calculating an integral:

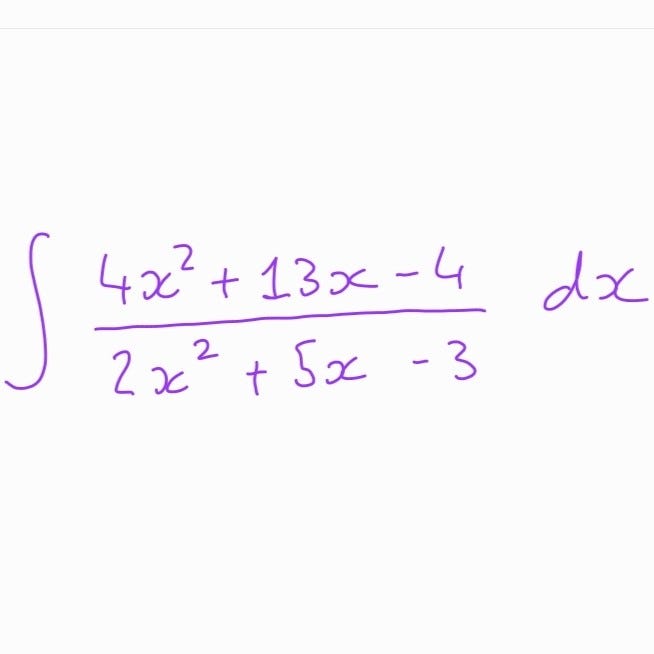
Hint: Consider utilizing partial fractions.

Feel free to attempt it on your own; the solution is provided below.

At the end of a lecture, two students approached me, expressing that they had approached the problem using different methods, resulting in two distinct answers. They were puzzled as to which method might have been incorrect. In a light-hearted moment, I jokingly remarked, “If you both arrived at different answers, at least one of you must be mistaken.”

With this assumption, I began reviewing both methods, anticipating that I would uncover a flaw in one of their approaches. Surprisingly, both methods seemed correct upon inspection, which led me to believe that one of the students had simply made a numerical error. I spent over ten minutes searching for this oversight, convinced it had to be present and that I was merely overlooking it. I was genuinely perplexed.

Eventually, it struck me: could it be that one of the students was actually correct? Almost immediately, I recognized the root of the issue. Let me present the two methods used by the students; perhaps you will notice the discrepancy more quickly than I did.

Both students applied the method of partial fractions and reached the conclusion that:

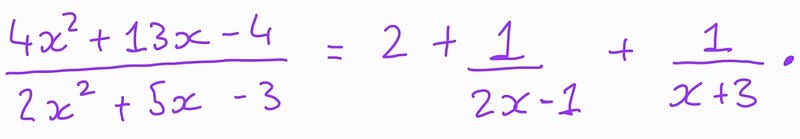
If you’re unfamiliar with partial fractions, don’t worry; it won’t hinder our discussion.

Following this, Student 1 proceeded to solve the integral by calculating:

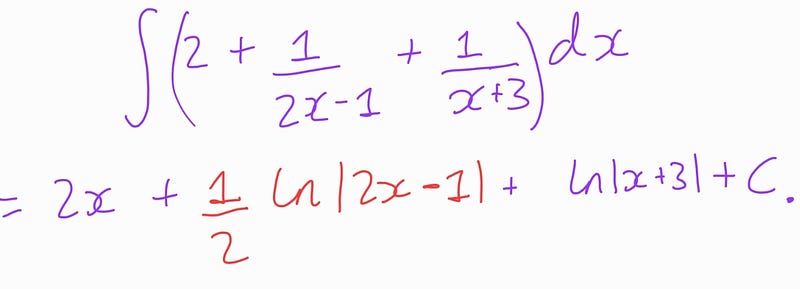
Student 2’s approach was nearly identical, but they took a factor of 2 out of the denominator in the middle summand first:

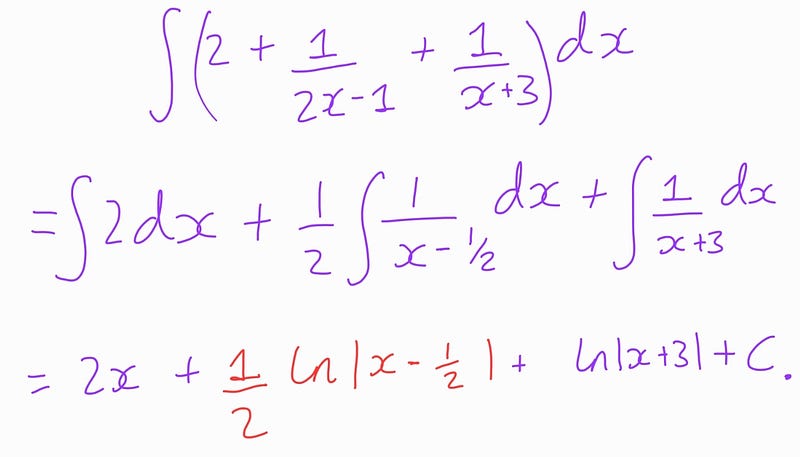
Thus, it appears that their answers align, except for the second summands highlighted in red. This led both students, and myself, to believe there must have been an error somewhere in the calculations. In reality, the only misunderstanding stemmed from assuming the answers were different.

When learning integration, we are taught never to forget our “plus C,” which represents the constant of integration. This concept often becomes routine, and while we understand that the constant is arbitrary, we sometimes neglect that our choices for C may differ.

This was precisely what happened: both students and I assumed that the representation of the constant of integration, C, was identical for both. However, that was not the case!

Referring back to our logarithmic rules, particularly:

we can re-express:

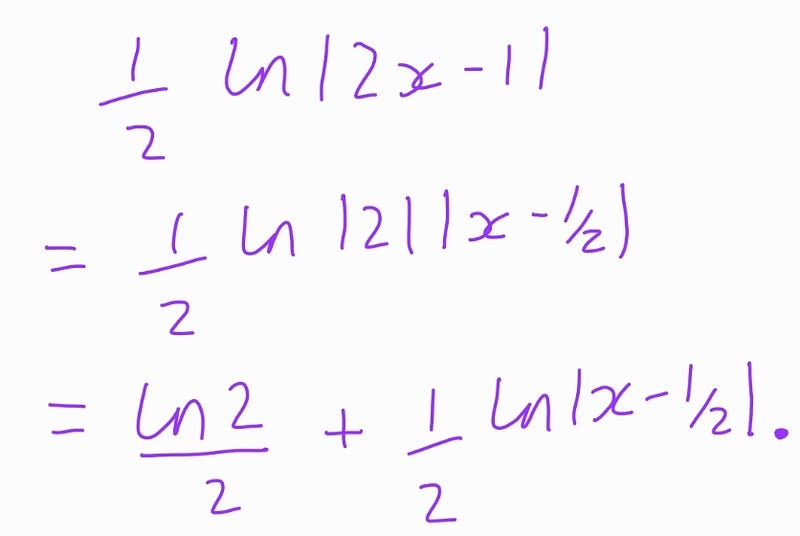
We can then restate Student 1’s solution as follows:

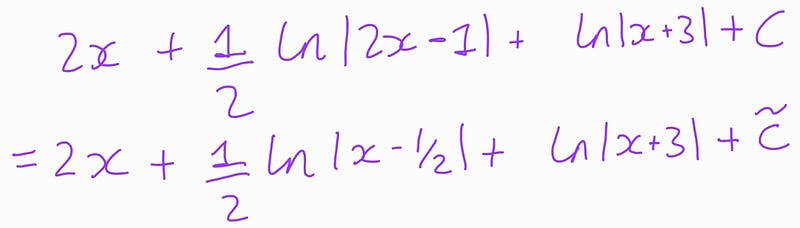
where

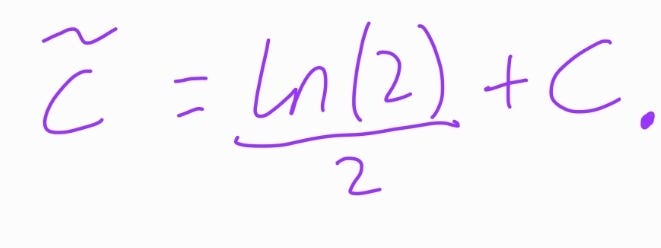
Consequently, we see that neither student was incorrect; they simply had different representations of their constants of integration. I had made an erroneous assumption and sought a problem that did not exist. While many of you may have recognized my mistake right away and think I should have avoided it, I am grateful for the experience. It helped me identify an issue I had not previously considered students might encounter.

In learning integration, I can confidently say that almost no student would think to re-write constants of integration to reconcile their answers. This incident has provided me with an excellent example to illustrate when such re-writing may be necessary, while also emphasizing that all antiderivatives (the solutions of an integral) of a function are equivalent up to the addition of a constant.

If you're interested, you can find all questions from this series, along with a discussion of my inspiration for the series, here.

Thank you for reading. I would greatly appreciate it if you considered following my publication, Y(Math), so my articles can reach a broader audience. If you wish, you can join Medium using my referral link and support myself and other writers you enjoy.

Chapter 2: Engaging with Integration

The video titled "Fast, Easy and FUN! 2 to 12 Times Tables" discusses engaging methods for learning multiplication tables, demonstrating the importance of foundational skills in mathematics.