Chapter 1: Introduction to the Physics Exam

Having just completed my first A Level physics examination, I can relate to the overwhelming stress and anticipation that exams evoke. Engaging in discussions with fellow students about our answers can be one of the more intriguing aspects of the exam experience. In my physics test, several questions seemed to leave many of my peers perplexed. I would like to present one of these questions to you, along with my approach to solving it. (Please note that the numbers in my example may vary slightly from the actual question due to my tendency to forget specifics!)

I can only imagine that even Einstein might have found this question somewhat straightforward, or perhaps he would have crafted a more challenging one!

The Question

Below is a common fusion reaction involving Deuterium and Tritium, both isotopes of Hydrogen.

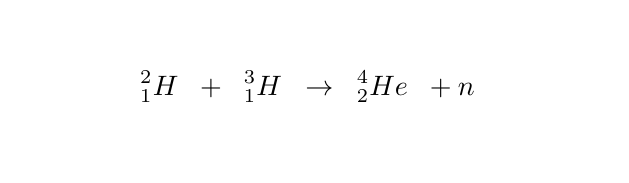
Given that the Deuterium and Tritium atoms remain stationary just before the fusion event, demonstrate that the kinetic energy of the neutron is approximately 80% of the total energy transferred to the Helium and neutron. (2 marks) If the total energy transferred to the Helium and neutron is 10.5 MeV, calculate the neutron's speed immediately following the reaction. (2 marks) Additionally, we will assume that protons and neutrons possess an equal mass of 1.67×10^-27 kg, and we will disregard any relativistic effects.

Challenge yourself with this problem before reviewing my solution. I found the first part to be more demanding than the second. Note that if you struggle with part one, the information provided there can assist in tackling part two.

Section 1.1: Analyzing Part 1

A critical observation in this problem is the statement that "the Deuterium and Tritium atoms are stationary just before the fusion reaction." This hints at the importance of energy conservation and momentum in the analysis.

To maintain momentum, the neutron and Helium atom must move in opposite directions with equal momentum, given that the total momentum before the reaction is zero. By leveraging this principle and recognizing that the mass of the Helium nucleus is roughly four times that of the neutron, we can express the velocity of the Helium atom in terms of the neutron's speed. This allows us to formulate the total kinetic energy in terms of just the neutron's speed.

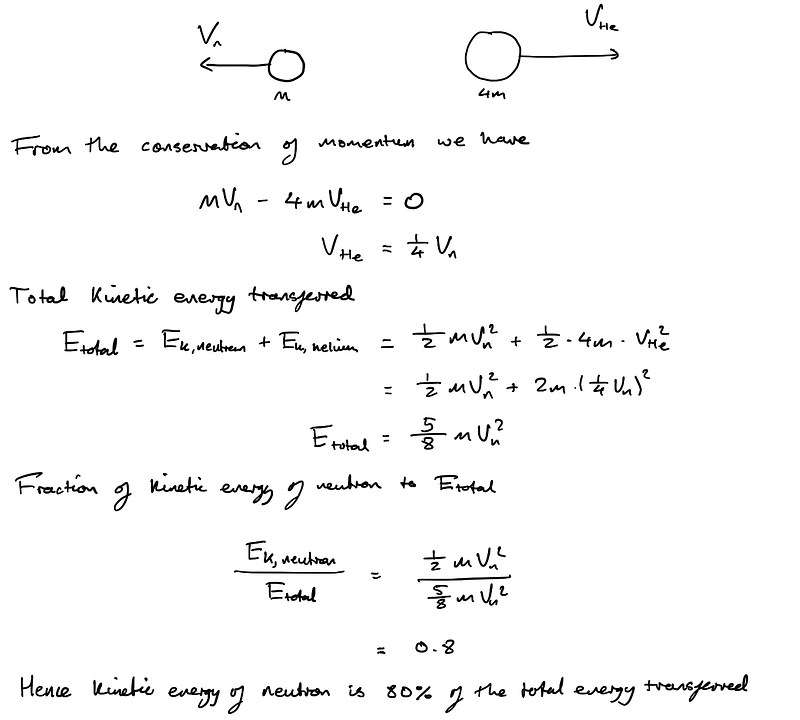
The challenge likely arises from applying momentum principles in atomic reactions.

Subsection 1.1.1: Moving to Part 2

In this section, we simply utilize the 80% concept derived from part one to determine the neutron's kinetic energy and subsequently find its speed. As long as we remember how to convert electron Volts to Joules, we should be fine.

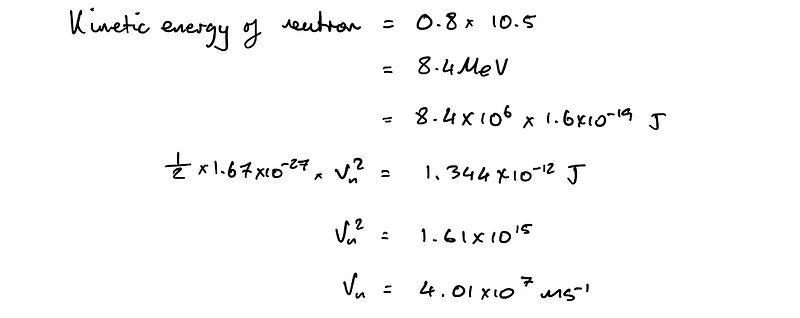
And there you have it! I trust you found the question engaging and appreciated the approach we took to solve it.

Chapter 2: Further Resources

For additional insight into challenging physics questions, consider watching the following videos:

Analyzing the most difficult physics questions from the past decade, focusing on their intricacies.

A comprehensive review of AP Physics 1, covering all seven units essential for mastering the subject.

Thank you for engaging with this content! If you have any reflections on the problem discussed, please share your thoughts.