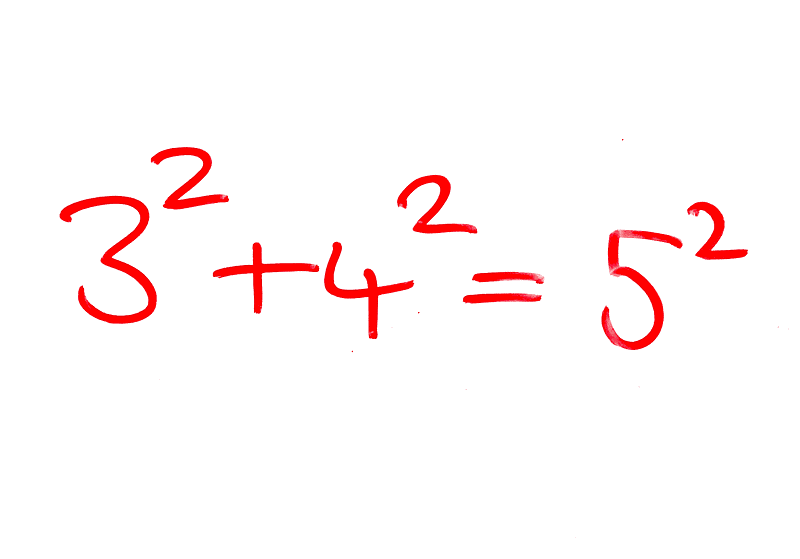How to Create Pythagorean Triples: Solutions to x² + y² = z²
Written on
Chapter 1: Introduction to Pythagorean Triples
Recall the well-known equation x² + y² = z² from your school days, often linked to Pythagoras' theorem for finding the sides of a right triangle. This equation has intrigued mathematicians who seek positive integer solutions, known as Pythagorean Triples.
For instance, the set (3, 4, 5) serves as a classic example since 3² + 4² equals 5². Moreover, from any Pythagorean Triple, such as (3, 4, 5), we can derive an infinite number of others by multiplying the entire set by a constant. For example, multiplying by 2 yields (6, 8, 10), which is also a valid Pythagorean Triple. It's a worthwhile exercise to explore why this property holds true.
A primitive Pythagorean Triple is defined as one where the numbers x, y, and z share no common factors greater than 1. The example (3, 4, 5) is considered primitive.
Section 1.1: Formulating Pythagorean Triples
A significant challenge in mathematics is to derive a formula for generating Pythagorean Triples. Enter Euclid’s Formula, which states that for any integers m and n (where m > n > 0), the following equations will produce a Pythagorean Triple:
- x = 2mn
- y = m² - n²
- z = m² + n²
For example, if we take m = 5 and n = 1, we arrive at the Pythagorean Triple (10, 24, 26). We can confirm this since 10² + 24² = 100 + 576 = 676 = 26².
The first video titled "Generating Pythagorean Triples (TANTON Mathematics)" elaborates on the method for creating these triples. It visually explains the concepts behind the formula and provides examples for better understanding.
Section 1.2: Validating Euclid's Formula
To ensure that Euclid's Formula is reliable, we can perform a quick verification:
x² + y² = 4m²n² + (m² - n²)² = 4m²n² + m² + n² - 2m²n² = (m² + n²)² = z².
However, simply presenting this formula lacks depth without comprehending its derivation. Let's explore how to derive Euclid's Formula from first principles.
By rewriting x² + y² = z² as x² = z² - y² = (z - y)(z + y), we can deduce that x/(z - y) = (z + y)/x. Since x, y, and z are positive integers, x/(z - y) represents a rational number. Recall that a rational number can be expressed as m/n where m and n are integers greater than 0.
We can establish the relationship:
x/(z - y) = (z + y)/x = m/n, leading to two derived equations:
- (z - y)/x = n/m
- (z + y)/x = m/n.
Adding these equations gives us 2z/x = (n² + m²)/mn, allowing us to set x = 2mn and z = n² + m². By subtracting the second equation from the first, we find 2y/x = (m² - n²)/mn, allowing us to set y = m² - n².
Thus, we have successfully derived Euclid’s formula for generating Pythagorean Triples under the condition that m > n > 0:
- x = 2mn
- y = m² - n²
- z = m² + n²
Chapter 2: Conclusion
Euclid’s Formula provides a means to demonstrate that x² + y² = z² has no solutions within natural numbers, which ties into the broader topic of Fermat’s Last Theorem.
The second video, "Formula for Generating ALL Pythagorean Triples," delves deeper into the formula and its applications, enhancing understanding of this fascinating mathematical concept.