The Emergence of Two-Tower Models in Recommender Systems

The principal aim of ranking models in recommender systems is to enhance relevance; that is, to predict the most suitable content based on context. Here, "context" encompasses all insights gathered about the user, drawn from their prior engagement and search histories, tailored to specific applications.

Nonetheless, these ranking models often display certain observational biases, notably position bias—the inclination for users to engage more with items presented first. The innovative approach behind two-tower models involves training two parallel neural networks: one for relevance and another for capturing various observational biases within the data. The logits from both towers are subsequently combined to generate final predictions, as illustrated in YouTube's "Watch Next" paper:

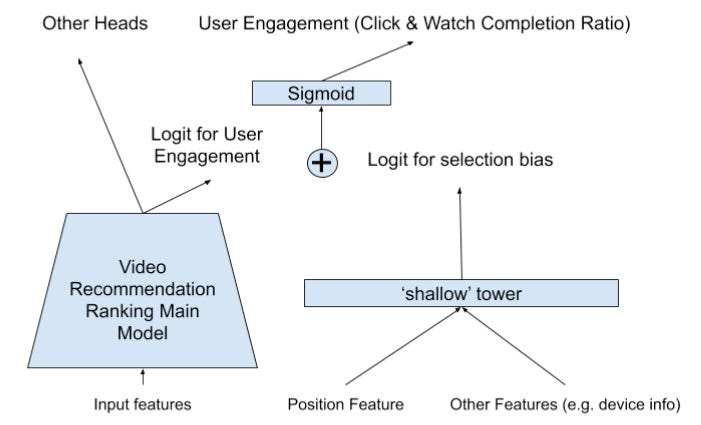
(Zhao et al. 2019)

The core idea is that by assigning a dedicated tower to biases, the primary tower can concentrate on its main goal of predicting relevance. Empirical evidence supports the efficiency of two-tower models, with significant improvements in various applications:

• Huawei's PAL saw a 25% increase in click-through rates in its App Store.
• YouTube's two-tower additive model enhanced engagement rates by 0.24%.
• Airbnb's implementation resulted in a 0.7% rise in booking rates.

In essence, two-tower models enhance ranking models by differentiating between relevance and bias, yielding notable advancements across the industry.

Section 1.1: The Factorization Assumption

Two-tower models rely on the factorization assumption, which assumes that click predictions can be expressed as:

p(click|x,position) = p(click|seen,x) × p(seen|position, ...).

This breaks down into the probability of a click based on whether the item was seen by the user (the first factor), multiplied by the likelihood of the item being observed based on its position and other features. YouTube reformulated this as a sum of logits, which is conceptually similar:

logit(click|x,position) = logit(click|seen,x) + logit(seen|position, ...).

However, this assumption falters when considering diverse user behaviors. For instance, suppose our training data includes two distinct user types:

• Type 1 users consistently click the first item due to impatience and a desire for immediate gratification.
• Type 2 users tend to scroll through options until they find exactly what they want, displaying patience and selectivity.

In this scenario, the factorization assumption collapses because p(seen|position) varies across user segments, which the current model fails to accommodate.

Instead of relying on factorization, alternative strategies have emerged as proposed in Google's recent paper, "Revisiting Two-tower Models for Unbiased Learning to Rank": the dot-product model and the Mix-EM model.

The dot-product model introduces a new approach, where the two towers produce embeddings instead of probabilities or logits, combining them via a dot product:

p(click|x,position) = Dot(relevance_embedding, bias_embedding).

This method allows for a more nuanced representation of biases across different user types.

The Mix-EM model, on the other hand, employs multiple two-tower models (the authors suggest two) and utilizes the Expectation-Maximization (EM) algorithm. In the E step, training examples are assigned to one of the two models, while in the M step, the overall loss across both models is minimized. This approach enables distinct models to accommodate different user segments effectively.

Both algorithms were tested in production within the Google Chrome Web Store, yielding results such as a +0.47% improvement in NDGC@5 for the dot-product model and a +1.1% increase for the MixEM model, in comparison to the standard two-tower additive model. These findings validate that the factorization assumption is inadequate for this context, highlighting the performance deficits stemming from its limitations. The dot-product and MixEM models offer more expressive frameworks for modeling the interplay between the two towers.

Section 1.2: The Independence Assumption

The second assumption underlying the conventional two-tower model is that the position of an item is independent of the items displayed in adjacent positions. However, as argued in the recent Google paper "Cross-Positional Attention for Debiasing Clicks," this assumption does not hold true in real-world scenarios. Click probabilities are influenced not only by the item presented but also by neighboring items, particularly in contexts where items are arranged both horizontally and vertically, like in the Google Chrome Store.

To address this limitation, the authors introduced XPA, or cross-positional attention. The methodology involves integrating inputs from neighboring items into both the bias and relevance towers. Specifically, the bias tower receives input not just from the current item's position but also from all adjacent items, represented as a single embedding. Likewise, the relevance tower processes not only the feature vector for the current item but also those for neighboring items.

The challenge lies in representing neighboring items with a single embedding, accomplished through a cross-attention layer that calculates attention weights using a scaled softmax:

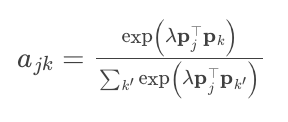
The embeddings of neighboring items are then computed as a weighted sum based on these attention weights:

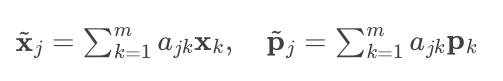
An architectural diagram illustrating this process shows how the two towers utilize multiple items simultaneously, considering all neighboring items during their computations:

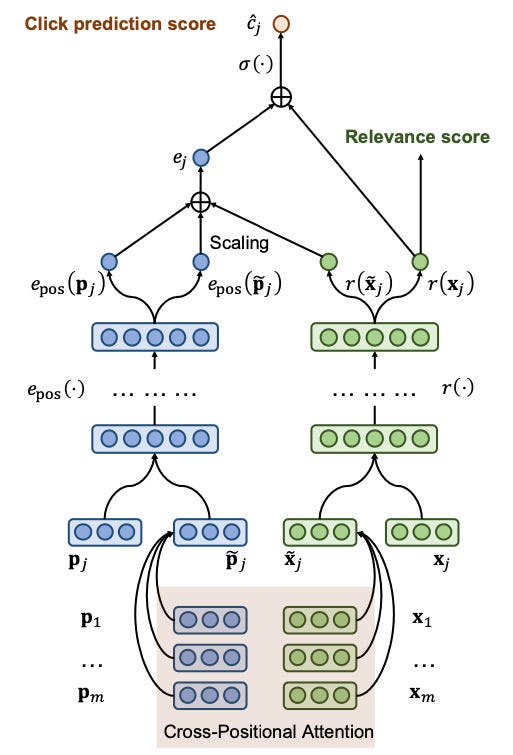
(Zhuang et al. 2021)

The final prediction results from a combination of four components: the outputs from the relevance towers (for both the item and its neighbors) and the outputs from the bias towers (again, for both the item and its neighbors), all adjusted using a sigmoid function.

Evaluating the results on production data from the Chrome Web Store revealed an +11.8% increase in click-through rates for XPA compared to a baseline that disregarded position and a +6.2% improvement compared to the traditional two-tower model. This substantial enhancement demonstrates the efficacy of considering not only an item's position but also the nearby items that influence user engagement.

The cross-attention matrix further illustrates this, with off-diagonal elements indicating the necessity of cross-attention to accurately model the data. A standard two-tower model would only account for diagonal elements, neglecting the interdependencies present among neighboring items.