Mastering Complex Integrals Using Substitution Techniques
Written on
Chapter 1: Introduction to Substitution in Integration
When tackling challenging integrals, the method of substitution proves to be an invaluable strategy. This technique is particularly useful for transforming integrals that may initially appear complex into simpler forms, making them easier to solve. In this article, I will present two intriguing examples that showcase the effectiveness of substitution in integration.
Integral Example 1
The first integral may seem straightforward at first glance, as we know that integrating an exponential function results in the function itself multiplied by a constant. However, the presence of a 1 added to exp(ax) in the denominator complicates the process of finding the antiderivative. Fortunately, we can simplify the evaluation through a strategic variable substitution.
Suppose we utilize the substitution:
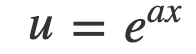
With this substitution, the derivative of u with respect to x is given by:

Next, we need to adjust the limits of integration to correspond with our new variable u. Given that the original limits in x are 0 and infinity, we find:
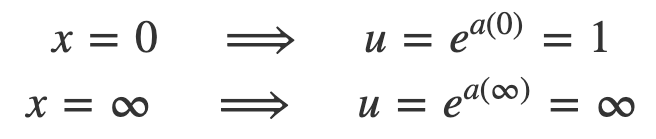
Consequently, the integral is reformulated as:
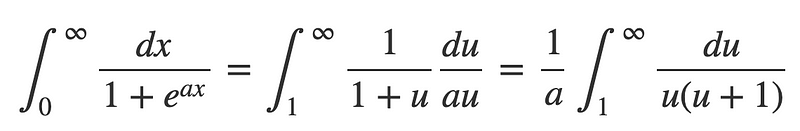
This expression can then be approached through partial fraction decomposition, where we let:
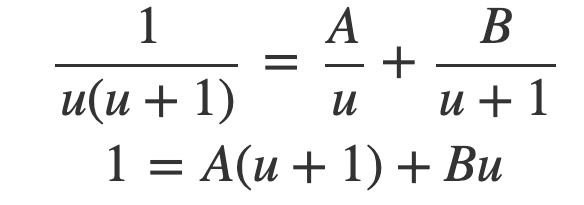
We identify the roots of u, which correspond to the factors u(u+1), specifically u=0 and u=−1:
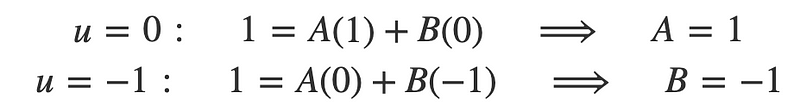
This leads us to:
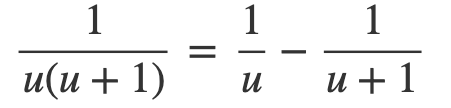
Thus, we have:
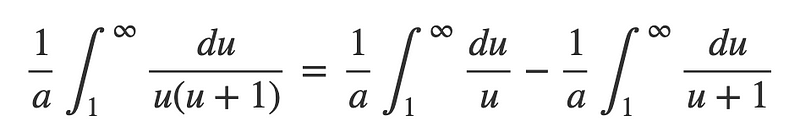
Each of these integrals simplifies to a natural logarithm:
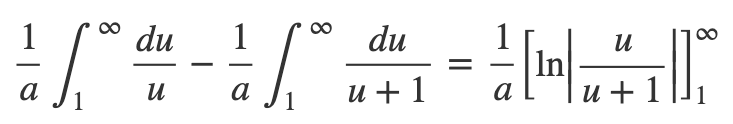
Evaluating the upper limit, we can express the argument in the logarithm as follows:
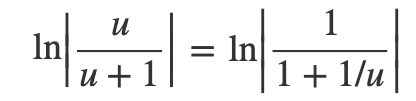
This reveals that substituting u = infinity results in 1/1, yielding ln|1| = 0. The lower limit is straightforward, leading us to the final result:
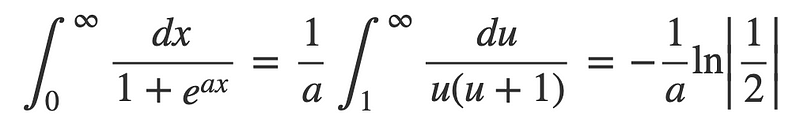
This expression can be further simplified by separating the logarithm:
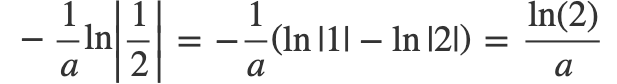
Thus, we conclude:
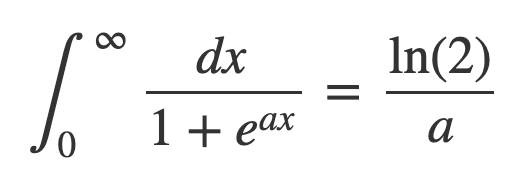
Integral Example 2
In this second example, a variable substitution may not be immediately apparent. However, we can leverage the representation of hyperbolic functions as combinations of exponential functions. For instance, cosh(x) can be expressed as:
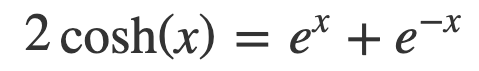
This leads us to:
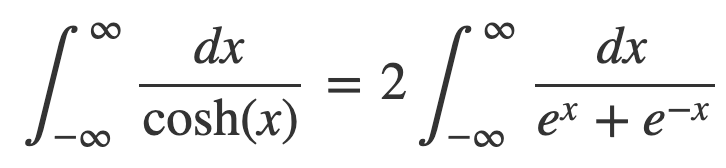
Next, we attempt the substitution:
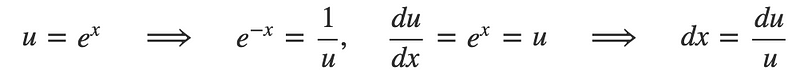
With this substitution, the limits become:
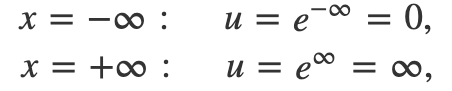
Thus, the integral is rewritten as:
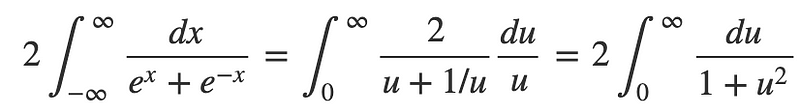
The final integral can be derived from standard integration tables:
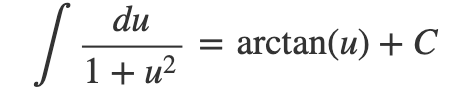
Consequently, we arrive at:
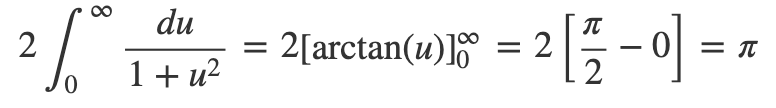
Thus, we conclude:
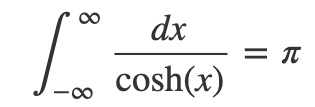
In this video titled "U-Substitution - More Complicated Examples," viewers will encounter various complex examples showcasing the u-substitution method in detail.
The video "21 Challenging u-Substitution Integrals (Antiderivatives)" offers a comprehensive look at a variety of challenging integrals that can be tackled using substitution techniques.