Chapter 1: Theoretical Foundations

The Christensen-Sinclair factorization theorem may seem like an enigma reserved for mathematicians, yet its significance extends far and wide. This crucial theorem, essential in operator space theory, demonstrates that intricate mathematical structures can be decomposed into simpler, more digestible components. Imagine it as a jigsaw puzzle, where one can visualize the complete picture without needing to fit every piece together. This factorization is more than a theoretical notion; it serves as a practical instrument for mathematicians and computer scientists, enhancing problem-solving efficiency.

A New Horizon

Semidefinite programming (SDP) represents a sophisticated evolution of linear programming, capable of addressing a wider array of challenges while maintaining computational efficiency. The allure of SDP lies in its potential to tackle problems beyond the reach of traditional methods. By employing SDP, researchers have validated that the Christensen-Sinclair theorem is not merely a theoretical abstraction but a functional tool. This relationship signifies that previously insurmountable issues can now be approached successfully, paving the way for advancements in areas such as quantum computing and information theory.

The Core Principle

At the center of semidefinite programming lies the concept of strong duality. This principle asserts that under specific conditions, the optimal solutions for a problem and its dual are identical. Although it may seem abstract, this concept is revolutionary. Understanding one side of a problem allows us to glean insights into the often more intricate counterpart. Within the framework of Christensen-Sinclair factorization, strong duality offers a clear and efficient route to tackle previously unsolvable problems, establishing itself as a fundamental aspect of contemporary computational theory.

Real-World Impacts

The practical ramifications of these theoretical advancements are immense. From enhancing algorithm efficiency in computer science to facilitating groundbreaking discoveries in physics, the Christensen-Sinclair factorization and SDP are reshaping our understanding and interaction with complex systems. These methodologies empower researchers to create innovative technologies and resolve real-world challenges with greater efficacy. Envision a scenario where computational power is so optimized that tasks once requiring extensive hours or days can now be executed in mere minutes. This represents the potential of applying these advanced mathematical principles in real-world contexts.

To visualize the significance of these mathematical innovations, consider the following graph illustrating the increase in computational efficiency achieved through semidefinite programming compared to traditional approaches.

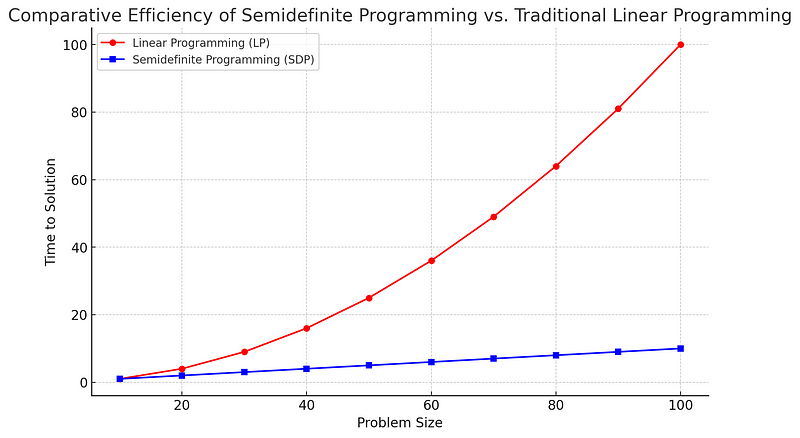
The Efficiency of SDP

Semidefinite programming is adept at modeling a diverse range of problems and solving them to arbitrary precision. This adaptability renders it an invaluable tool for mathematicians and computer scientists striving for exact solutions to intricate challenges. The capability to address a broader class of problems than linear programming alone makes SDP essential in modern computational mathematics.

Chapter 2: Quantum Computing and Beyond

The first video delves into the strong duality in linear programming and its applications in gradient descent methods. It explores how these concepts intertwine to enhance computational strategies.

The second video features Varghese Mathai discussing T-duality for loop spaces at the "M-Theory & Math 2023" conference, shedding light on its implications for quantum computing.

Christensen-Sinclair in Quantum Computing

The Christensen-Sinclair theorem finds its place in quantum computing, a domain poised to transform our information processing capabilities. By defining quantum query complexity, researchers can formulate algorithms that exploit the unique characteristics of quantum mechanics, potentially yielding breakthroughs in speed and efficiency for problem-solving.

The Broad Reach of Strong Duality

Strong duality transcends a single discipline; its principles permeate various fields, including economics, engineering, and physics. This universality suggests that advancements in our comprehension of strong duality may trigger cross-disciplinary innovations, fostering progress across multiple sectors.

Constructive Proofs Without Hahn-Banach

The proof of the Christensen-Sinclair factorization theorem presented in the research circumvents the Hahn-Banach theorem, a key but abstract element in functional analysis. Instead, it employs more elementary principles from linear algebra, rendering the proof more accessible and constructive, which can lead to practical algorithmic applications.

Algorithmic Efficiency

Algorithms derived from semidefinite programming for computing the completely bounded norm are not only efficient but also scalable. This scalability ensures that as our computational challenges expand, our methodologies remain effective and reliable.

Embracing Mathematical Innovation

The transition from abstract mathematical theories to tangible applications exemplifies human creativity and the power of collaborative research. By leveraging the capabilities of semidefinite programming and grasping the profound implications of the Christensen-Sinclair factorization, we are forging a path toward a future where complex problems are solvable and innovative technologies emerge. This relentless pursuit of innovation inspires not only those within the scientific community but also future generations to explore, discover, and innovate.

About Disruptive Concepts

Welcome to @Disruptive Concepts — your crystal ball into the future of technology. Subscribe for new insight videos every Saturday!

Watch us on YouTube